Cadence企业命题专项奖设置

• 一等奖一队，奖金10 000元
• 二等奖三队，奖金5 000元

三维集成电路的多层模块划分最优化算法

背景

• 一个数字电路的Verilog网表通常由多个模块（module）组成。模块内部的逻辑单元、寄存器之间有大量的连接。模块和模块之间也互相有信号的连接。当设计者在早期规划芯片的布图结构(Floorplan）的阶段，通常可以先忽略模块内部的连接，而更关注模块之间的连接关系。这样可以在不损失太多精度的同时，更快速地评估架构的可行性。
• 同时我们也需要考虑各个模块的面积（通常由该模块内部instance的总面积决定），使得这些模块在后端实现的布局布线阶段，能够在芯片的版图上得到合理的面积分配。
• 此处为了简化问题的形式，我们暂时忽略整个芯片对外的输入输出（I/O)而只考虑模块之间的连接。

例如，图1是拥有7个模块（Verilogmodule，非hardIPblock）的一个芯片。模块有不同大小的面积。模块之间的连接用线段表示，线段上的数字代表了连接的信号个数。

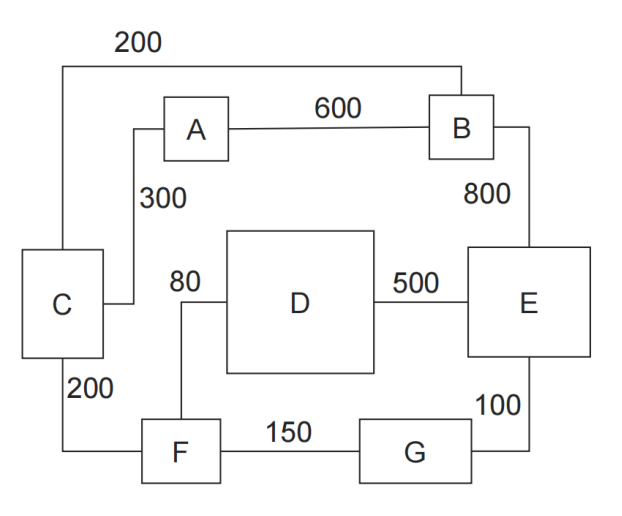
图1:模块大小和连接关系的例子

三维集成电路与模块划分

用三维集成电路来实现一个芯片，会遇到的一个常见问题是：如何对整个芯片的电路模块进行划分，使这些模块被分配到多个裸片（Die）上。

下图是一个把电路划分成两部分，并分配到上下两个同样面积的裸片上的例子。划分之后，两部分电路之间的连接，通过裸片之间的堆叠工艺实现，比如常见的有Bump以及TSV（ThroughSiliconVia）。

图2:划分到两个裸片的例子

关于TSV

TSV提供了信号穿越裸片衬底的通路。但是它自身也需要占据一部分面积，因此也必须考虑到TSV带来的额外的面积需求。

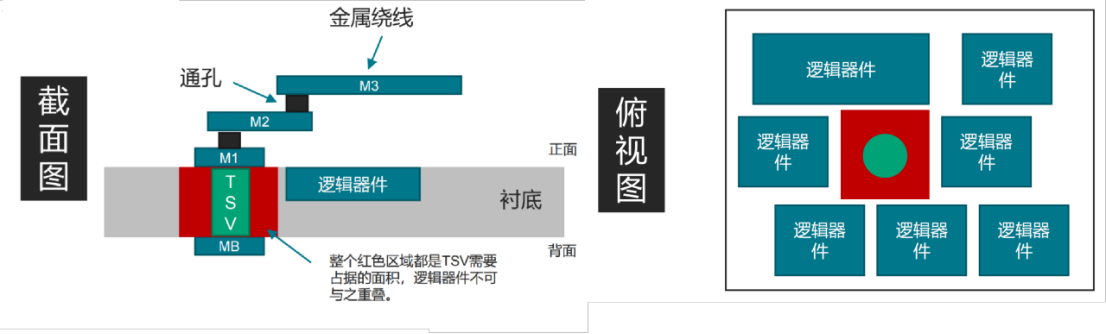
图3:TSV示例

当多层裸片堆叠时，凡裸片和裸片界面处穿过衬底的地方需要TSV。

图4:多层裸片间的TSV

关于Feedthrough

当多层裸片堆叠时，比方说3层：从第一层到第三层的信号连接，即使在逻辑上并没有和第二层的模块有任何关系，物理上也必须穿过第二层，即Feedthrough。从而有可能会产生额外的TSV。

图5:Feedthrough

约束条件

三维划分需要考虑的硬性约束条件有：

1.一个裸片上所有模块的总面积，加上这个裸片上所需的TSV的总面积，不能超过裸片的面积，即面积利用率不能超过100%。

2.相邻两个裸片的界面上，可容纳的Bump/TSV的数量是有上限的。

约束条件的例子

下图是面积约束条件的一个例子（假设每根线代表100个信号）：

如果不考虑面积，左边的划分是最好的，因为只需要200个bump。但是第一层的模块总面积已经超过了裸片面积。

此时采用右边的方案，bump数量增加到了500个，但只要仍然小于两个die之间所能容纳bump数量的上限，同时模块总面积也并没有超过裸片面积，则仍然是可行的。

题目要求

对于主办方给定的：

• 模块连接图（包含模块面积以及连接关系和信号数量）
• 裸片尺寸、TSV单位尺寸
• 相邻两个Die之间的Bump/TSV数量上限（为简化题目，假设Bump和TSV的数量上限相同
• 附件下载链接：http://cpipc.acge.org.cn/sysFile/downFile.do?fileId=9858fd164ecd47ae9fa8ac5d767e1304

要求把所有模块划分到3个裸片上。不考虑整个芯片对外的I/O。堆叠方向如图所示，灰色表示衬底：

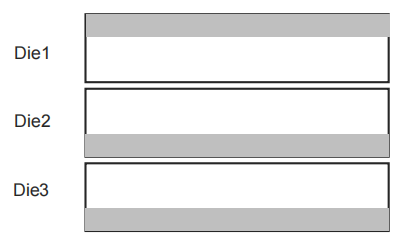
图7:堆叠方向

在满足硬性约束条件下，最优化以下两个目标：

1.3个裸片上模块的面积利用率尽可能相同。避免出现有些裸片过于拥挤而有些裸片大片空白的情况。利用率=（模块总面积+TSV总面积）÷裸片面积

2.裸片间bump/TSV数量尽可能少。

附加题——考虑模块布局与总线长

基本题并不考虑模块在版图上的具体位置，只计算其面积和连接数。附加题要求提出一种算法并尝试实现：在考虑模块布局（无缝铺满整个裸片区域，形状可以是矩形或直角多边形，如图8所示）的前提下，使总线长最短。

注1：由于利用率总是小于100%，因此铺满后每个模块的占地面积将大于它的初始面积。但不可小于初始面积。

注2：总线长的计算用模块几何中心之间的水平距离来简化。

注3：TSV假设均布在裸片上，可先不考虑其具体位置，但面积需算入。

图8:模块布局与总线长

提交要求：

1. PPT报告，2. 优化算法代码，3. 可重现的计算结果